Why Is Matrix Math Different in Every Graphics Program?

What gives?

So this is you: You're picking up some 3D software, hear the word "matrix" thrown around, and do some research.

You initialize the same 4x4 translation matrix in Unreal Engine and Godot, and aside from coordinate-system differences, they behave identically. You decide to multiply it with a rotation matrix... and they both behave differently! Unreal does "translate then rotate", but Godot does "rotate then translate"!

"That's weird", you say to yourself. "I guess some programs just do it backwards. Good to know."

But then you initialize that same 4x4 translation matrix in Blender's Python REPL... and it doesn't even do anything!

"Is this a bug in Blender?" you say, mildly annoyed.

After experimenting, you find that transposing the matrix works in Blender.

But it's not a bug in Blender, or in any of them.

Here's why

There are different conventions for representing transformation matrices. The authors of various 3D packages decide to use one convention over another. It really just boils down to that.

I present two core properties that define matrix transformations in different programs:

1. Element order: Row-major vs Column-major order
2. Transform style: Post-multiply column-vector ($y=Ax$) vs Pre-multiply row-vector ($y=xA$)

Element order: Row-major vs Column-major order

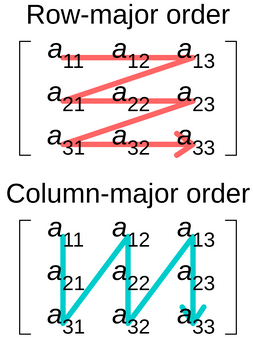
From the Wikipedia article: https://en.wikipedia.org/wiki/Row-_and_column-major_order

Row-major and column-major order answers the question: "How do we describe a matrix as a flat list of numbers?"

Given the 4x4 matrix:

We can write it as row-major:

float A[16] = {1,0,0,5, 0,1,0,10, 0,0,1,15, 0,0,0,1};

Or as column-major:

float A[16] = {1,0,0,0, 0,1,0,0, 0,0,1,0, 5,10,15,1};

When we talk about row-major and column-major order, it can be in the context of the memory layout of the particular matrix data structure or how it's indexed. Alternatively, it can be how it's initialized from code. I find the latter more useful in most contexts.

Note that element ordering virtually never describes a visual representation of a matrix. If you're pretty-printing a matrix or you see one in a user interface and it's arranged in rows and columns, then they're rows and columns!

With row-major of column-major order, the math doesn't change. It only affects the way it's represented as a flat list.

Transform style: $y=Ax$ vs $y=xA$

We use the notation $y=Ax$ and $y=xA$ to refer to two distinct transform styles.

$y$ describes an output vector, $x$ describes an input vector, and $A$ describes a transformation matrix. Please do not confuse $x$ and $y$ with the x and y axes.

When we say $y=Ax$, we post-multiply with a column vector. The operation looks like this:

When we say $y=xA$, we pre-multiply with a row vector. The operation looks like this:

Both examples represent a rotation on the Z axis by 90 degrees (positive), followed by a translation of (10,20,30). The results of both are equivalent vectors, just transposed.

Notice that the matrices are transposed, and that the order is reversed. Composing longer chains of transforms works this way too. This owes to the fact that in linear algebra, transposing a product will "reverse" the order of the factors and transpose those factors. i.e. $(ABC\cdots Z)^T = Z^T \cdots C^TB^TA^T$ (the "shoes and socks rule")

Pros of $y=Ax$:

• The most common style in mathematics and math textbooks.
• Order is the same as functional composition. If we use functions $f$ and $g$ to describe transformations, then $f \circ g$ is the same as $f_{matrix} \cdot g_{matrix}$

Pros of $y=xA$:

• Might be more computationally performant if stored in row-major ordering.
• Order is left-to-right. You read transformations as they are applied from local to world.

How do you test how a program does matrix transformations?

We need to figure out both transform style, and element order.

The test I like to use for transform style is to multiply a translate with a scale:

Because the matrices will evaluate to one of the two:

The translation for Case 1 is $\langle 10,20,30 \rangle$, while the translation for Case 2 is $\langle 20,40,60 \rangle$.

Other methods certainly work, as long as the two transforms don't commute. For example, a rotation and a translate works, because they don't commute: $rotate \cdot translate \ne translate \cdot rotate$. But a rotation and a scale doesn't work, because they do commute: $rotate \cdot scale = scale \cdot rotate$.

The transform style is $y=Ax$, if and only if (any of):

• The translation vector is a column
• The basis vectors are columns
• A point is transformed by post-multiplying a column vector
• $\mathrm{translation}(\mathrm{translate}(10,20,30) \cdot \mathrm{scale}(2)) = \langle 10,20,30\rangle$
• Composition happens in right-to-left order (assuming local to world)
• $translate \cdot scale =$ a scale, followed by a translation
• $translate \cdot scale$ leaves the translation unaffected

The transform style is $y=xA$, if and only if (any of):

• The translation vector is a row
• The basis vectors are rows
• A point is transformed by pre-multiplying a row vector
• $\mathrm{translation}(\mathrm{translate}(10,20,30) \cdot \mathrm{scale}(2)) = \langle 20,40,60\rangle$
• Composition happens in left-to-right order (assuming local to world)
• $translate \cdot scale =$ a translation, followed by a scale
• $translate \cdot scale$ changes the translation

Testing the element order is easiest if you know the transform style and how a matrix is initialized:

Note that the left cells above are pseudocode for a matrix that translates by (10,20,30).

Some APIs will group into vectors, while others will make you provide a flat array of numbers.

$y=Ax$ and $y=xA$ don't affect basic matrix operations

Those two styles only prescribe how transform matrices are created. Given known matrices, it doesn't actually affect the basic matrix operations and the order of their arguments.

For example, for matrix multiplication, the order only swaps because the matrices themselves are not the same in the different programs.

No matter which style a program uses, the following operations should remain identical across them.

• Transpose: $A^T$
• Matrix multiplication: $AB$
• Inverse: $A^{-1}$
• Determinant: $\det A$
• Minor: $M_{i,j}$
• Cofactor: $C_{i,j}$
• ... and pretty much all of them

Appendix: a table of matrix transform conventions for popular programs

The results of this table are all my own independent research. I've tried and tested the code in the table. Feel free to fact-check!

cube.matrix_local = Matrix( ((1,0,0,10),(0,1,0,20),(0,0,1,30),(0,0,0,1)) )

cmds.setAttr('pCube1.offsetParentMatrix', [1,0,0,0, 0,1,0,0, 0,0,1,0, 10,20,30,1], type='matrix')

@P = @P * {1,0,0,0, 0,1,0,0, 0,0,1,0, 10,20,30,1};

out = c4d.Matrix(off=c4d.Vector(10,20,30), v1=c4d.Vector(1,0,0), v2=c4d.Vector(0,1,0), v3=c4d.Vector(0,0,1)) * pos

matrix4d xformOp:transform = ( (1,0,0,0), (0,1,0,0), (0,0,1,0), (10,20,30,1) )

SetActorTransform(FTransform(FMatrix({ 1,0,0,0 }, { 0,1,0,0 }, { 0,0,1,0 }, { 10,20,30,1 })));

transform = Transform3D(Vector3(1,0,0), Vector3(0,1,0), Vector3(0,0,1), Vector3(10,20,30)) * transform

transform:matrix3d(1,0,0,0, 0,1,0,0, 0,0,1,0, 10,20,30,1)

gl_Position = worldViewProj * mat4(1,0,0,0, 0,1,0,0, 0,0,1,0, 10,20,30,1) * pos;

output.position = mul(mul(float4(input.position,1), float4x4(1,0,0,0, 0,1,0,0, 0,0,1,0, 10,20,30,1)), worldViewProj);

glm::vec4 out = glm::mat4(1,0,0,0, 0,1,0,0, 0,0,1,0, 10,20,30,1) * in;

XMVECTOR out = XMVector3Transform(in, XMMATRIX(1,0,0,0, 0,1,0,0, 0,0,1,0, 10,20,30,1));

Eigen::Vector4f out = Eigen::Matrix4f({ {1,0,0,10},{0,1,0,20},{0,0,1,30},{0,0,0,1} }) * in;

* Cinema 4D: The translation vector is the first column, and we effectively multiply with the column vector $\begin{bmatrix}1,x,y,z\end{bmatrix}^T$. See: https://developers.maxon.net/docs/Cinema4DPythonSDK/html/manuals/data_algorithms/classic_api/matrix.html#matrix-fundamental

** Godot: The Transform3D class is a composite of Basis vectors and an Origin vector, which is effectively column-major. The "tscn" scene file stores a flat list of the elements of a 3x4 matrix in column-major order.

* Note: Initialization order describes how a matrix is created from scratch. This describes the element order for numbers passed to a class constructor, function, array, or inline syntax. It's usually the same as storage order, but not always (Eigen is an example of this).

The work is not shown, but "Transform style" is based on other indications such as built-in transform functions and the order that transforms are applied (e.g. "translate", "rotate", "scale"). GLSL and HLSL are "by convention", because they don't include transform functions and they allow for both $y=Ax$ and $y=xA$. GLSL and HLSL conventions are based on the old (deprecated!) transform stacks built into OpenGL and DirectX respectively.