Yes.
For decades, we've asked ourselves "Can it run Doom?". Now we can finally make the ultimate punchline: "Can Doom run it?"
I demonstrate that it is possible to run any bounded computation in Doom, minus constraints on level size. I have not proven that Doom is Turing complete (see the section later in this article).
This works with the vanilla MS-DOS release of Doom 2 (v1.9). No mods or anything!
I love projects like these. I was inspired by the esoteric machines in other games such as Minecraft and RollerCoaster Tycoon.
Demonstration
Source code
If you're curious about how this works, I released the source code to build the map here:
https://github.com/nukep/doom-calculator
Related projects
Updates: 2022-12-23, 2022-12-24, 2022-12-26
I'm reading online comments, and several folks have pointed out other equally impressive attempts that have been made to demonstrate computation in some Vanilla and non-Vanilla engines! I'll update this list periodically.
- Game of Life in BOOM: https://www.doomworld.com/forum/topic/131881-conways-game-of-life-in-boom/
- Doom in Doom: https://www.youtube.com/watch?v=c6hnQ1RKhbo (technically it's an arbitrary code execution exploit, but still cool)
- https://calabi-yau.space/blog/doom.html (Logic gates using lifts in Vanilla Doom. I originally linked to them at the end of the article)
- Voodoo script: https://doomwiki.org/wiki/Voodoo_script (mostly BOOM and conveyor belt floors, but with some Vanilla Doom capabilities)
- Ripple-carry adder in BOOM: https://www.youtube.com/watch?v=pvji3DJNnqE, https://www.doomworld.com/idgames/levels/doom2/Ports/a-c/counter
NAND: The universal logic gate
My first exploration into this topic was to implement a NAND gate. If I could implement NAND, I knew I could implement anything.
NAND is a universal logic gate. In short, universal logic gates can be composed to create all possible logic gates.
NAND truth table:
| a | b | result |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
e.g. if a is True and b is True, the result is False.
Specifically, NAND represents two on/off inputs, and one on/off output. If both inputs are on, then the output is off. If any of the inputs are off, then the output is on.
It turns out that from just a measley logic gate, you can combine NAND - you can feed NAND into other NANDs - and you can create any truth table. In effect, all bounded computations are possible.
My process to figuring out if this was workable in Doom was to play around with a Doom level editor - namely, SLADE. I just had to implement one NAND gate. After lots of experimentation with lifts, actions, teleporters, switches, doors, monsters, and even duplicate players, I found a system that was simple and robust.
Binary Decision Diagrams
A consequence of my findings was that my system could represent any boolean logic as described in a binary decision diagram.
We can represent NAND from earlier using a binary decision diagram.
There are two nodes for variables a and b. The dotted lines represent off, or 0. The solid lines represent on, or 1.
If we start at "a" and "a" is 0, then we will go left and arrive at the result of "1" and our work is done. But, if we start at "a" and "a" is 1, then we go right and we arrive at "b". If "b" is 0, then the result is "1". If "b" is 1, then the result is "0".
We could decide to chain NANDs together and create even more complex diagrams. But in my case, I decided not to merely chain NANDs together, because this doesn't create very efficient diagrams. In practice, we're better off chaining together other logic gates such as AND, OR, XOR, etc - or to directly convert a truth table to a diagram.
As a Doom level
Visual of a NAND gate (a=1, b=0):
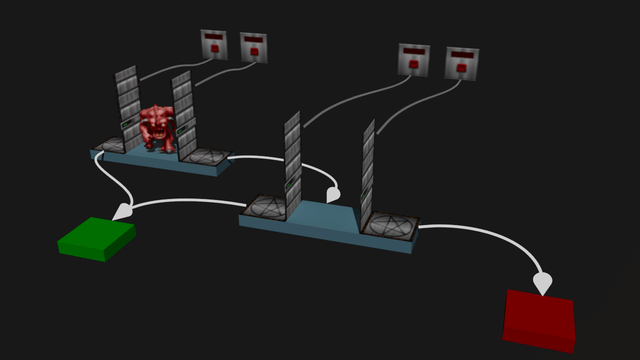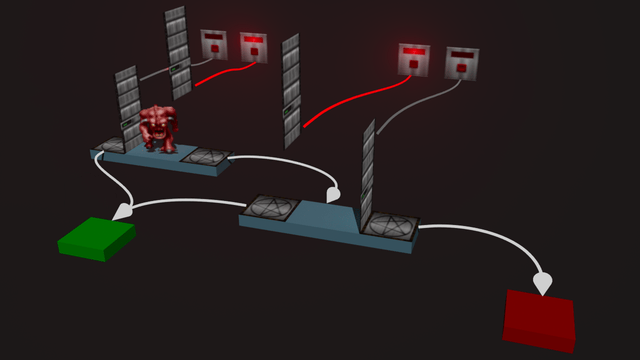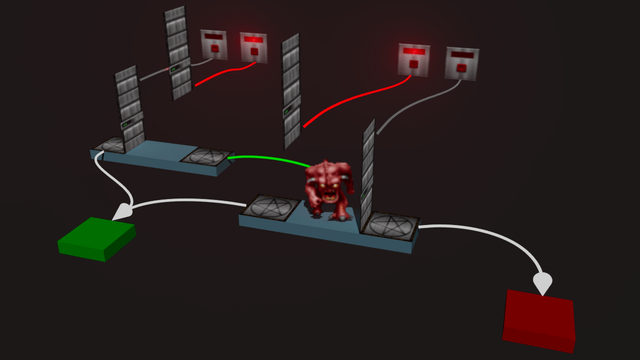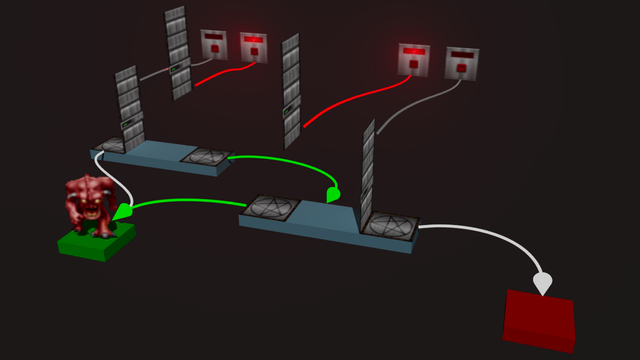
Binary decision diagrams can be represented in Doom in a very straight forward manner.
A node becomes a small room, with two doors for 0 and 1. Root nodes have monsters in them.
An edge of a node becomes a teleportation from a teleporter behind a door to another room, if that door is to be opened.
The doors are opened by switches activated by the player. They can also be opened by other monsters (I explain why this is useful later).
I made the decision to represent 0 and 1 with two switches each. At first it might seem more logical to have a single switch for each variable. But I found it easier to be explicit about setting a variable to 0 or 1, and for the calculation to wait until they're set.
In the final calculator WAD, I do have individual switches for each digit, but this is nothing more than a visual illusion. These are secretly variables where the 0/1 pairs are split into two digits each: (0,1) -> a; (2,3) -> b; (4,5) -> c; (6,7) -> d; (8,9) -> e. E.g. "6" means "d=0", "7" means "d=1".
How do we add numbers with this?
It can be difficult to imagine how monsters teleporting to places can represent addition. This is one of those problems that's easier to understand in smaller pieces going bottom-up.
We went from NAND, and then to binary decision diagrams. Next, let's try adding two binary digits.
There are two binary digits: 0 and 1.
The rules for addition over binary digits are:
| a | b | carry | sum | in other words |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 + 0 = 0 |
| 0 | 1 | 0 | 1 | 0 + 1 = 1 |
| 1 | 0 | 0 | 1 | 1 + 0 = 1 |
| 1 | 1 | 1 | 0 | 1 + 1 = 0, carry the 1 |
We can also decide to interpret the above rules as a truth table. This is known as a half-adder.
A half-adder is equivalent to the logic gates:
- carry = a and b
- sum = a xor b
This is great for adding two binary digits... but we want to add bigger numbers!
It's entirely valid to combine lots of half-adders together to create an adding machine. But in practice it's more efficient to implement distinct logic to add 3 bits: two numbers and a carry bit. This is known as a full-adder.
i.e. with three terms such as: "1 + 0 + 1 = 0, carry the 1".
A full-adder is equivalent to the logic gates:
- carry = (a and b) or (b and c) or (c and a)
- sum = a xor b xor c
It's now possible to chain a half-adder with many full-adders to create an n-bit-adder (where n is how many bits we want). It works just like traditional addition: Add two numbers, then carry the 1 over to the left pair of digits, then add those, and so on.
We're interested in adding numbers from 0 to 9. How do we represent that? It turns out we need at least 4 binary digits to represent the numbers from 0 to 9 (where 0 = 0000, and 9 = 1001). Therefore, we use a 4-bit-adder.
There's a major issue however, and it's that we want to display results in base 10, and not binary or hexadecimal.
We remedy this by conforming the results of a 4-bit binary adder. The resulting logic is known as a BCD adder (binary-coded decimal adder).
If the result is greater than 9, then add 6. Apply modulo 8 to it. Finally, set the carry bit.
This way, an operation like "9 + 5 = 14" would yield "1001 + 0101 = 0100, carry the 1".
BCD adder pseudocode:
# 4-bit binary addition
# result is carry bit, then sum bits
zc,z3,z2,z1,z0 = cin + (a3,a2,a1,a0) + (b3,b2,b1,b0)
# if the result of the 4-bit binary adder is > 9, set the carry-out "cout" bit
cout = zc or (z3 and z2) or (z3 and z1)
# Add 6 (0110) modulo 8 to the 4-bit binary addition if it's > 9
s0 = z0
cc1, s1 = z1 + cout # half-adder (2 terms)
cc2, s2 = cc1 + z2 + cout # full-adder (3 terms)
_, s3 = cc2 + z3 # half-adder (2 terms)
The resulting (unoptimized) binary decision diagram looks like this (input variables are colored blue, temporary variables are colored yellow):
To recap: The above diagram represents adding two digits from 0 to 9, and getting a 0 to 9 digit with carry.
There are multiple trees to facilitate this. Some will set variables whose sole purpose is to be used in other subsequent trees.
To visualize the above diagram with monsters and teleporters, the top of each tree (the root node) will have a monster in it. All non-root nodes will be destinations for monsters. There are 14 monsters in total, for 14 trees.
Linking outputs to variables
In order to compose diagrams from many smaller diagrams, it's useful to say "this output should be a variable". You may have noticed that the BCD adder depends on this.
The version of this in a Doom level is "a monster going through a teleporter should open other doors".
In vanilla Doom, monsters can't activate switches or remote-open doors. What I've decided to do instead, is exploit a quirk in the Doom engine. All doors are associated with a sector. If a door shares a sector with another door, then the two doors will always open and close together. Monsters can't open remote doors, but they can open local doors. If that local door shares a sector with other doors, then monsters can remotely open doors!
So in place of a final destination, a monster teleports to a room with a single door that they're forced to keep open. That door shares a sector with one or more other doors that will then be opened.
There are various limitations to this quirk. For example, shared sectors must have the exact same floor and ceiling textures, as well as heights. Fortunately this doesn't impede functionality, so we're good with it. Many Doom level editors (such as SLADE) also try to "unshare" sectors if you try to edit distinct polygons, so if you're editing the map afterwards, it requires caution.
Digit displays
I figured that just showing binary values was too boring. I had to drive the point home and go big with showing actual numbers.
The way I approached the digit displays, was to create a truth table for each pixel of the display.
A number from 0 to 9 can be represented with 4 binary digits (0/1). For example, I'll take the pixel at row 1 column 2 and show its truth table. Note that for readability I'm condensing 4 inputs into one column of the table.
| bits 3210 | out |
|---|---|
| 0000 (0) | 1 |
| 0001 (1) | 0 |
| 0010 (2) | 1 |
| 0011 (3) | 1 |
| 0100 (4) | 0 |
| 0101 (5) | 1 |
| 0110 (6) | 1 |
| 0111 (7) | 1 |
| 1000 (8) | 1 |
| 1001 (9) | 1 |
| 1010 (10) | undefined |
| 1011 (11) | undefined |
| 1100 (12) | undefined |
| 1101 (13) | undefined |
| 1110 (14) | undefined |
| 1111 (15) | undefined |
This can be expressed as the following binary decision diagram:
There are binary values 10 thru 15 that are undefined, because we're not expected to encounter them. The algorithm I wrote to generate the diagram will assign arbitrary outputs for 10 thru 15, depending on which optimizes the diagram more. (in practice, for digits, "bit 3=1" just refers to 8 and 9. if 8 and 9 have the same result, we know the result for "bit 3=1")
Generating the level with code
I didn't make the adding machine in a level editor. Doing it all manually would be extremely tedious and error-prone. So I wrote code!
The code to generate the WAD file is written in the programming language Clojure.
Lisp abides by the code-is-data philosophy, so it's quite intuitive to write tree structures as code.
We can represent the NAND gate from earlier using Lisp syntax.
;; a NAND b:
(a 1
(b 1
0))
This is a tree data structure. It's composed of nested lists in the form of (variable on-0 on-1).
We can also visualize this as a sideways tree that reads left-to-right:
But the really really cool part, is that this works doubly as code. If a and b are functions that return the left or right form, you can actually execute this and get a result!
;; function that returns right
(defn a [left right] right)
;; function that returns left
(defn b [left right] left)
(a 1
(b 1
0))
;; returns 1
We can implement more complex logic in a very succinct syntax:
;; Full adder
;; Tree 1: Sum bit
(cin (a (b 0 1)
(b 1 0))
(a (b 1 0)
(b 0 1)))
;; Tree 2: Carry bit
(cin (a 0
(b 0 1))
(a (b 0 1)
1))
The implementation of those functions depends on what you're trying to do. In my case for generating levels, all functions for variables emit an adjacency list for a graph, where the nodes are identified by auto-incrementing numbers.
Many binary decision diagrams are not trees, however, but graphs. Nodes in a binary decision diagram can have more than one parent. How do we express graphs?
This is actually a deceptively easy problem to solve. If we assert that all trees are immutable mathematical values, then we can say whether or not two trees are equivalent. Equivalent trees are deduplicated, effectively creating graphs in memory.
Optimizing trees
I use a variety of techniques to optimize trees:
- If a tree "a" points to trees "b" and "c" and b = c, then a = b = c
- If a variable "v" is only used once anywhere, is in a root tree "a" and the tree points to trees "b" and "c", then v.0 = b and v.1 = c
- Remove all trees that don't eventually contribute to outputs (where monsters would show up).
Optimization 3 was one I chose to implement using adjacency matrices. Where K is an adjacency matrix of trees to trees, I compute K^0 + K^1 + K^2 + ..., which gives us a final result of all reachable trees. The code for it is here: https://github.com/nukep/doom-calculator/blob/e3dd9c0c6de19830febd0d1f845befca70ad632d/src/doomcalc/tree.clj#L217
Drawing the level
Doom's level format is WAD. WAD officially stands for "Where's All the Data?" according to Tom Hall's "Doom Bible".
Despite the game being 3D, Doom maps exist on a flat 2D cartesian plane. Height is achieved by defining variable floor and ceiling heights for polygonal shapes in the map (Doom calls these shapes "sectors").
WAD is fortunately a very simple file format, so I was able to implement a WAD writer from scratch.
Because the levels are represented in 2D, routines to draw the level are similar to drawing vector graphics overall. E.g. "draw line from a to b".
Overcoming vanilla Doom quirks
I noticed that monsters opening doors worked in GZDoom, but it sometimes didn't work in Chocolate Doom or the vanilla MS-DOS Doom.
To figure out why, I did what any sensibly sane person would do: Look at the Doom source code. (everything else I've done has clearly been sane up to this point)
The official source code release for Doom from id Software can be found here: https://github.com/id-Software/DOOM
I Ctrl+F's some keywords such as "open" and "door", and eventually stumbled across the code where monsters try to open doors on their own.
I started from the P_Move() function here: https://github.com/id-Software/DOOM/blob/77735c3ff0772609e9c8d29e3ce2ab42ff54d20b/linuxdoom-1.10/p_enemy.c#L272
The procedure for monsters opening doors is the following, as pseudocode. I left out a lot of ireelevant details.
# p_enemy.c: P_Move()
def P_Move(actor):
# Direction is a unit vector. 1 of 8 possible directions (45 degree increments).
try_position = actor.position + actor.speed*actor.direction
actor_moved = False
# p_map.c: P_TryMove(), P_CheckPosition()
spechit = []
for each line within the actor radius from try_position:
# p_map.c: PITCheckLine()
# Note: lines are partitioned in blockmaps (128x128 sections of the level).
# Blockmaps are checked bottom-top, then left-right. (an "N" formation)
if line has no back face: break
if line blocks players or monsters: break
if line has a special action: spechit.push(line)
if loop did not break:
if new floor is within 24 units (not too high or low):
if actor can fit in the room:
move the actor to try_position
actor_moved = True
for each line in spechit, in reverse order:
if actor walks over line: trigger line
spechit = []
if not actor_moved:
for each line in spechit, in reverse order:
use line
spechit = []
These were the most important findings:
- The game searches for all special lines within the monster's radius, from where the monster is trying to go (not where it is).
- There's a global array that's appended with special lines "spechit". Up to 8 can be stored, but the game doesn't stop at 8 (possible buffer overflow).
- Blockmaps are searched in column-major order (bottom-up, then left-right)
- The iteration routine quits early if any line in reach of the monster has the "block players" or "block players and monsters" flag enabled.
- It also quits early if it finds a wall with no back face (such as the outer edge of the map).
To allow monsters to open door, we follow some rule-of-thumb restrictions:
- No lines with "block players/monsters" flags within monster radius+speed (for Pinky: 30.0 + 10.0 = 40.0 units)
- No one-sided lines (such as the map perimeter) within monster radius+speed (40.0 units)
- Keep any doors you don't want opened by a monster beyond monster radius+speed (40.0 units)
Interactive Demo: Digit displays
Press one of the buttons below to simulate the digit display.
This is true to what happens in the Doom map.
Does this mean Doom is Turing complete?
My observations didn't prove it. This would be an amazing claim though, because it would mean we could run anything, including Doom itself (well... if we removed map and memory limitations).
Update (2022-12-23): The "Doom-in-Doom" project uses an arbitrary code execution exploit to run Doom in Doom: https://www.youtube.com/watch?v=c6hnQ1RKhbo. It's incredibly impressive, so check it out! It's also worth noting that it doesn't rely on Doom's mechanisms to run logic, but cuts straight to the hardware and runs machine code (and definitely isn't portable outside of Vanilla or Chocolate Doom!).
To clarify, Doom is definitely functionally complete. That is, if we were to remove all the technical limitations, it can run all logic gates.
For Doom to be Turing complete, it has to allow some sort of unbounded looping construct.
My system is not Turing complete, and it's because it doesn't have unbounded loops and state. When monsters arrive at their destination, they stay there forever. There's no way to "reset" monsters. This can probably be done by selectively recalling (teleporting) certain monsters so they can act as input to the next iteration of the calculation. This is probably the next step to proving whether or not Doom is Turing complete.
Am I optimistic that it's Turing complete? Yeah! But it requires more work before we can confidently say so.
If it's eventually believed to be Turing complete, we can prove Turing completeness by implementing something that is. If we can implement Game of Life or Rule 110, then that would be sufficient proof. (I'm partial to Game of Life, because of the irony of "Game of Life" being in a video game about killing demons).
Update (2022-12-23: Game of Life does run in Doom! You need a newer BOOM-compatible engine to run it: https://www.doomworld.com/forum/topic/131881-conways-game-of-life-in-boom/
Someone else got logic gates in Doom, too!
So, I was actually working on this project on-and-off for two plus years. During it, Jared Candelaria beat me to it! Even had the same idea for the article title!
https://calabi-yau.space/blog/doom.html
Their approach was different from mine, and involves lifts and synchronizing with the timing of those lifts. They claim it's Turing complete, but I have doubts about this (similar to the reasons why mine isn't).
Download the WAD
If you're running it, I recommend a modern source port like GZDoom.
I also provide a version of the WAD that runs in the MS-DOS release of Doom 2 (v1.9), albeit with a lot of graphical glitches. But it's functional, and true to the limitations of vanilla Doom!
Here!